[Buru Ariketa] Zein urtetan izango ditu otsailak bost astelehen?
[Buru Ariketa] Zein urtetan izango ditu otsailak bost astelehen? –
Zientzia Kaiera atariak dozena erdi ariketa proposatu ohi ditu udarako, eta horrela egiteko asmoa du aurten ere. Abuztuan, astelehenero ariketa bat jarriko dute webgunean -jada eskegi dituzte batzuk-, eta irailean emango omen dituzte erantzunak.
EHUren Kultura Zientifikoko Katedraren blogak eredu bera erabili izan du aurreko bi urteetan ere, eta salabardoari iazko ariketak berreskuratzea otu zaio, oraindik egin gabe dituzun horrentzako. Igandero bat eskegiko dugu leiho honetan, aurreko ariketaren erantzunarekin batera.
Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta udako oporretan egiteko astero ariketa matematiko bat izango duzu; Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.
Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta datorren astean emaitza zuzenaren berri emango dizugu.
.
.
NOIZ IZANGO DITU BERRIRO OTSAILAK BOST ASTELEHEN? (6. ariketa)
Iaz otsailak bost astelehen izan zituen. Zein urtetan gertatuko da horrelakorik berriro? Hemendik ordura arte, zenbat bider izango ditu urtarrilak bost astelehen?
.
.
.
Bosgarren ariketaren erantzuna (neurrien bila):
Irudiko karratu txikiaren aldeak 16 cm ditu eta karratu handiarenak, 36 cm. Zenbat neurtzen du karratu ertaineko aldeak eta zein da goiko erpinaren altuera?
Hauxe da erantzun zuzena: 24 cm ditu karratu ertaineko aldeak eta 54 cm da goiko erpinaren altuera.
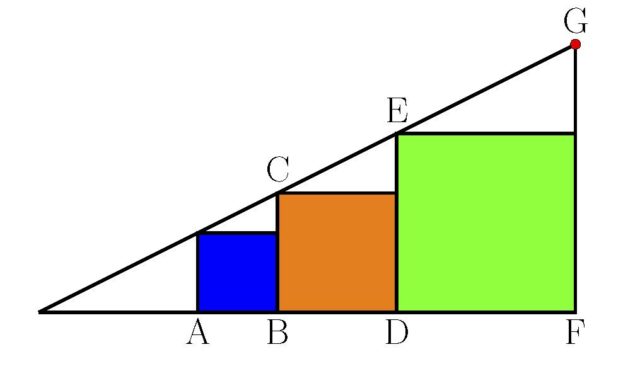
Izenak jarriko dizkiegu irudiko puntu batzuei, irudiak erakusten duen moduan.
Orain, antzekotasuna erabiliko dugu. Triangeluak erabil daitezke, Enekok aipatzen duenez, baina beste irudi batzuekin ere arrazoitu dezakegu. Adibidez, erlazio hauek ditugu:
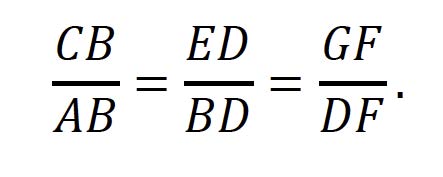
Badakigunez AB=16, ED=36 eta CB=BD direla, lehen berdintzatik BD=24 aterako dugu. Ondoren, bigarren berdintza erabiliz, GF=54 lortzen dugu.
.
______________________________________
Azken ariketa hau, seigarrena, ez dago “Calendrier Mathématique 2016. Un défi quotidien” delako egutegitik hartuta, baina zerikusi handia du egutegiarekin.
[Buru Ariketa] Zein urtetan izango ditu otsailak bost astelehen?
