Javier Duoandikoetxeak, EHUko Analisi Matematikoko Katedradun erretiratuak, Zientzia Kaieran.

Martxoaren 14a Matematikaren Nazioarteko Eguna da. Bigarren urtez ospatuko da eta bigarrenez eragingo dio pandemia egoerak. 2020an, dena prest zegoenean, bertan behera geratu ziren hainbat ekitaldi, Parisen egitekoa zen hasiera-ekitaldi nagusia barne. Aurten, egoera aurreikusita, online egiteko antolatu dira ekitaldi asko. “Matematika mundu hobe baterako” goiburua du 2021eko ospakizunak, matematika Covid-19ari aurre egiteko erabil daitekeela iradokiz, besteak beste.

Ospakizunaren jatorria Pi eguna da. 1988an Larry Shaw fisikaria egun seinalatu hori ospatzen hasi zen San Frantzisko hiriko Exploratorium museoan. Pi zenbakiaren dezimal biko adierazpen ezaguna —3.14— data bihurtuz, martxoaren 14a da, hirugarren hilabeteko 14. eguna, alegia. Denborarekin ospakizuna zabalduz joan zen eta azken hamarkadan mundu guztira egin zuen salto. Gure artean ere izan dira ekitaldiak Pi egunaren aitzakiarekin. Dataren arrakasta ikusita, Matematikaren Nazioarteko Eguna izenda zezala eskatu zioten UNESCOri eta hark 2019ko azaroan onartu zuen. Horregatik, duela urtebete egin zen lehen ospakizuna izen berriarekin, “matematika nonahi” goiburu hartuta.

Artikulu honen helburua ospakizunari baino jatorrian duen pi zenbakiari buruzko zenbait kontu jakingarri azaltzea da.

.

Zer da pi?

Hori bera gertatu zitzaidan Satorrari, Matematiketako irakasleari, pi zer zen galdetu nionean, eta berak «hiru, hamalau, hamasei» zela erantzun zidanean, hori erantzun bat balitz bezala.

Miguel Delibes, Kastila zaharreko kontu zaharrak (Patxi Apalategik euskaratua)

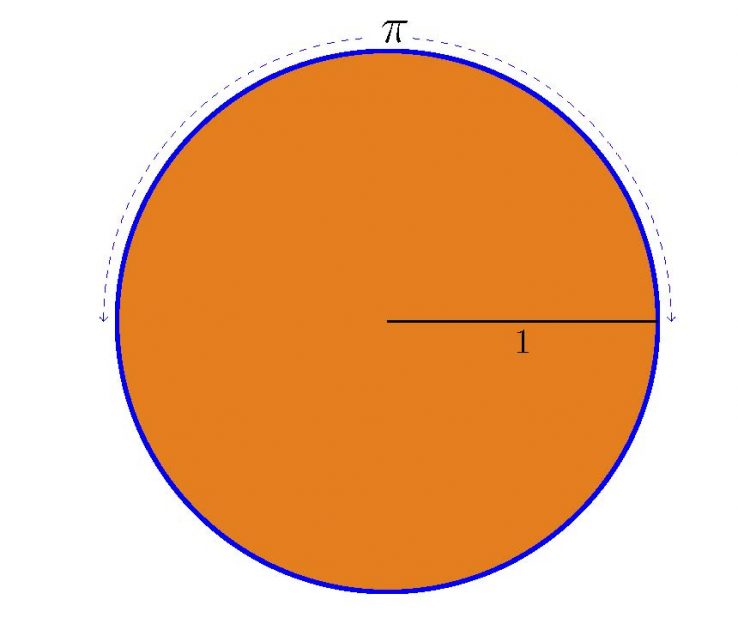
Argi zebilen Delibesen ipuineko mutikoa, pi delako horrek fama badu, ez baita izango “3-14-16” izateagatik, zerbait sakonago beharko du atzean. Eta hala da, noski. Zirkunferentzia baten luzeraren eta haren diametroaren arteko erlazioa (zatidura) bera da edozein delarik horretarako erabiltzen dugun zirkunferentzia. Zenbaki berezi hori  letra grekoaz adierazten dugu, eta, horregatik, pi du izena.

Era berean, zirkulu baten azalera eta haren erradioaren karratuaren arteko erlazioa ere zenbaki bera da. Zenbaki hau eta aurrekoa bat datozela, hots, hau ere dela, frogatu egin behar da. Arkimedesen emaitza batetik, esaterako, ondorioztatzen da hori, beherago erakutsiko dugunez.

.

Zergatik

Aipaturiko erlazio horrek ez zeukan izen berezirik. William Oughtred (1574-1660) ingelesa izan omen zen lehena letra erabiltzen hura adierazteko. Geroago, William Jones galestarrak 1706ko liburu batean erabili zuen. Letra greko hori alfabeto latinoaren p letrari dagokio eta periferia () hitzaren lehen letra delako aukeratu zuten. Leonhard Eulermatematikari handiak bere egin zuen proposamena eta haren lanek eragin nabarmena izan zutenez XVIII. mendetik aurrera, laster onartu eta orokortu zen erabilera. Handik aurrera da matematikako notaziorik ospetsuena.

.

= 3 izan zenekoa

Urthuz egin zuen halaber itsaso bat, hamar besokoa bazter batetik bertzera, inguruz biribila: haren goratasuna bortz besokoa zen, eta hogoi eta hamar besoko sokhatto batek birundatzen zuen inguruan.

Erregeak III, 7:23 (Jean Pierre Duvoisinek euskaratua)

Bibliako testu horren arabera diametroa 10 besokoa izanik, 30 besoko zirkunferentzia dugu. Hortaz, = 3 izango genuke. Biblia hitzez hitz hartzen dutenek agian arazoa izango dute matematikako klasean…

Testua K. a. VI. mendekoa omen da eta ordurako hori baino hobeto ezagutzen zen zirkunferentziaren eta diametroaren arteko erlazioa. Batzuen iritziz, testu literario moduan irakurri behar da eta ez zaio inolako asmo zehatzik bilatu behar.

Honen harira, komeni da ohar bat paratzea: matematikako objektu abstraktuak idealak dira eta mundu errealean aurki ditzakegunak haien antzekoak izango dira, baina ez perfektuak. Horrela, praktikan zirkunferentzia baten eta diametroaren arteko zatidurak ezin digu inoiz -ren balio zehatzik eman ( = 3 baino hobea bai, seguruenik).

.

Rhind papiroa

Oso zaharra da ezagutzen dugun -ren lehen hurbilketa. K.a. XVI. mendeko Egipton agertzen da, zehazki Rhind papiroa izeneko dokumentuan. Zirkulu baten azalera bera duen karratu bat eraikitzeko bidea azaltzen da bertan, zilindro baten bolumena ematen duen formula baten barruan. Zirkuluaren diametroa bederatzi zati egin, bat kendu, eta beste zortzien luzerako aldea duen karratua da zirkuluaren azalera bera duena. Ez da zehatza, jakina.

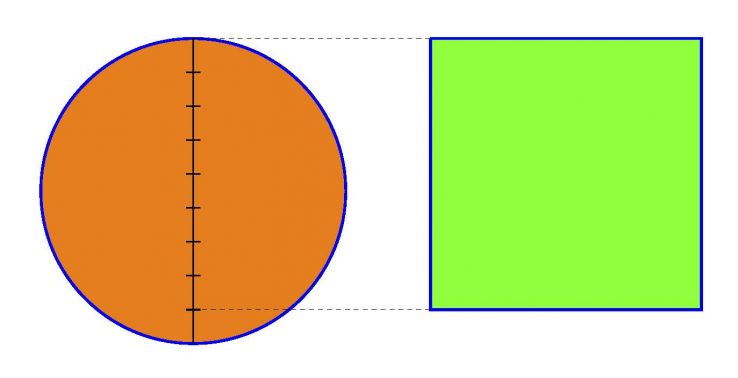
Ez da testuan inon aipatzen guk deitzen dugun zenbakia, antzinako matematikan irudien arteko erlazioak agertzen baitziren. Baina guk, emandako informazioarekin, lor dezakegu: zirkuluaren erradioa 9/2 izanda, hau dugu:

Noizkoa den kontuan hartuta, ez da batere hurbilketa txarra.

.

Arkimedes

K.a. III. mendean Sirakusan bizi zen antzinateko zientzialaririk handiena, Arkimedes. Haren lan ugarien artean bada Zirkuluaren neurketa izeneko eskutitz bat. Bertan, zirkuluaren azalera triangelu zuzen batenaren berdina dela frogatzen du. Triangelu zuzenaren kateto bat erradioa da eta bestea zirkunferentziaren luzera. Horren ondorioz, “zirkunferentziaren ” eta “zirkuluaren ” berdinak dira.

Gainera, zirkulua kanpotik eta barrutik poligonoen bitartez hurbilduta, goitik eta behetik bornatu zuen. Hau lortu zuen:

Oso hurbilketa ona da eta, bereziki, -ren balioa bi zifra dezimalekin 3.14 dela erakusten du.

-ren dezimalen kalkulua historia amaigabea da eta hobe dugu beste baterako uztea.

.

Zirkuluaren koadratura

Zirkulu baten erradioa emanda, eraiki erregela eta konpasa erabiliz zirkuluaren azalera bera duen karratuaren aldea. Antzinako Grezian hasi eta mendez mende erantzunik gabe bidaiatu zuen problema bat da hori. Erradioa unitate gisa hartuta, -ren erro karratuaren luzerako zuzenkia egitea eskatzen da, beraz. Problema baliokidea da luzerako zuzenkia eraikitzea.

Erabateko erantzuna ez zen XIX. mendera arte heldu:

• Johann Heinrich Lambert, 1761: irrazionala da, hots, ez da zenbaki oso biren zatidura.
• Ferdinand von Lindemann, 1882: traszendentea da, hots, ez da koefiziente osoak dituen ezein polinomioren erroa.

Irrazionala izatea lehen urrats modura uler daiteke, baina ez du eragozten eskatzen den eraiketa. Traszendentea izateak bai, ordea. Beraz, erregela eta konpasarekin zirkuluaren koadratura egitea ezinezkoa da, oraindik ere zeregin horretan gogoz saiatzen direnak badauden arren.

.

= 3.2 izateko zorian egon zenekoa

Indianako mediku batek, Edward J. Goodwin jaunak, zirkuluaren koadratura egiteko modu “berri” bat asmatu uste zuen XIX. mendearen amaieran. Estatuari oparitu nahi izan zion bere metodoa, hango irakaskuntzan dohainik (sic) erabiltzeko. Horrela, 1897an lege-proiektu bat prestatu zuten, zegokion ibilbide legala egin zezan. Ez zen bertan aipatzen, baina = 3.2 ateratzen zen, zirkunferentziaren luzerari begiratuz gero. Hortaz, lege-proiektua onartuz gero, balio hori izango zuen -k Indianako eskoletan.

Ordezkarien Ganbaran eztabaidatu behar zuten hasteko. Goodwin jaunak lortu zuen zenbait ordezkariren oniritzia proiektuak aurrera egiteko. Handik Senaturako bidea egin behar zuen. Zorionez, Purdue unibertsitateko irakasle batek jakin zuen zertan ari ziren eta astakeria galanta egiten ari zirela jakinarazi zien senatari batzuei. Azkenean ez zuten bozkatu, senatari batek ohartarazi baitzuen Ganbarak ez zuela eskumenik egia matematikoen gainean erabakiak hartzeko. Horrek ez zuen eragotzi ordezkari politikoak barregarri geratzea, garaiko prentsak erakusten duenez.

.

2021eko Matematikaren Nazioarteko Eguna

Utz dezagun eta itzul gaitezen martxoaren 14ko ospakizunera. “Matematika mundu hobe baterako” goiburua garatzeko web gune berezi bat prestatu dute eta bertan ikus daiteke matematikak hainbat arlotan duen erabilera. Era berean, iazko “matematika nonahi” ere beste web gune batean gordetzen da. Bietan informazio ugarirako sarbide interesgarriak aurkituko dituzue. Hemen inguruan ere ekitaldi eta dokumentu ugari aurki daitezke Martxoa, matematikaren hilabetea izenburupean (EHU eta BCAM daude babesleen artean). Gehiena gaztelaniaz dago, baina badaude material batzuk euskaraz ere.

PI = martxoak 14 (3/14) PI = martxoak 14 (3/14)