[Buru Ariketa] 2020ko azken erantzuna –

Zientzia Kaiera atariak dozena erdi buru ariketa atondu izan ditu azken udetan. EHUren Kultura Zientifikoko Katedraren blogak eredu bera erabili izan du aurreko urteetan ere, eta salabardoari, iaz egin zuen legez, aurreko urteko ariketak berreskuratzea otu zaio, 2018koak, oraindik egin gabe dituzuenontzako.

Igandero bat eskegiko dugu leiho honetan, aurreko ariketaren erantzunarekin batera.

Ariketa fisikoa egitea osasungarria dela esaten digute behin eta berriro. Fisikoa bakarrik ez, buruari eragitea ere onuragarria da. Nagiak atera eta udako oporretan egiteko astero ariketa matematiko bat izango duzu; Javier Duoandikoetxea matematikariak aukeratu ditu Zientzia Kaieran argitaratzeko. Guztira sei ariketa izango dira.

Gogoan izan ahalegina bera –bidea bilatzea– badela ariketa. Horrez gain tontorra (emaitza) lortzen baduzu, poz handiagoa. Ahalegina egin eta emaitza gurekin partekatzera gonbidatzen zaitugu. Ariketaren emaitza –eta jarraitu duzun ebazpidea, nahi baduzu– idatzi iruzkinen atalean (artikuluaren behealdean daukazu) eta datorren astean emaitza zuzenaren berri emango dizugu.

.

.

Seigarren ariketaren erantzuna (Luzeren bila):

6.- Paralelogramo baten azalera 36 cm² da eta diagonalen neurriak 12 cm eta 10 cm dira. Aurkitu aldeen luzerak.

Hurrengo irudiak erakusten duen notazioa erabiliko dugu.

Pitagorasen teorema eta azalerarako eman diguten informazioa erabiliz, ekuazio hauek ditugu:

Hirugarren ekuazioak h=36/a ematen digu. Bigarren ekuazioari lehenengoa kenduta, 4ad = 4, , edo ad = 11 dugu. Hortaz, d = 11/a. Lehenengo ekuazioan ordezkatuz,

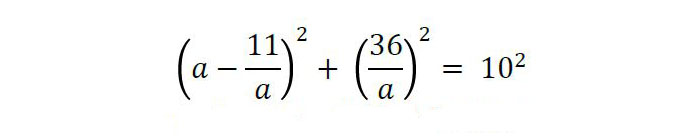
ekuazioa lortzen dugu, edo a⁴ – 122a² + 1417 = 0. Bigarren mailako ekuazioa dugu a² ezezagunerako, eta a² = 109 eta a² = 13 soluzioak ditu. Hortaz, a = ?109 edo a = ?13 izan daiteke. Beste aldea lortzeko, b² = d² + h² egingo dugu. Horrek b = ?13 ematen du, a = ?109 bada, eta a eta b-ren balioak trukatuta beste kasuan. Horrela, ?109 ? 10.44 eta ?13 ? 3.61 dira aldeen luzerak.

Bigarren bidea. Paralelogramo baten azalera kalkulatzeko formula hau dugu:

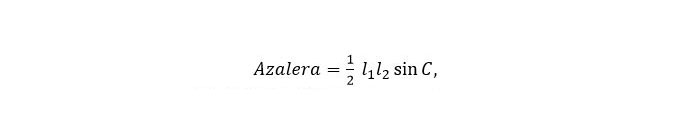
non l₁ eta l₂ diagonalen luzerak diren eta C diagonalen arteko angelua. Ariketak emandako datuak ordezkatuz, sin?C = 3/5 lortzen da. Aldeak kalkulatzeko diagonalen erdiek eta alde bakoitzak osatzen duten triangeluan kosinuaren teorema erabiliko dugu:

C angeluaren sinua ezagutzen dugunez, kosinua kalkulatzeko ez dugu angeluaren balioa behar, (sin?C)² + (cos?C)² = 1 baita. Orduan, cos?C = 4/5 eta cos?(180^o – C)= -4/5. Hortik, a² = 109 eta b² = 13.

______________________________________

Ariketak “Calendrier Mathématique 2017. Un défi quotidien” egutegitik hartuta daude. Astelehenetik ostiralera, egun bakoitzean ariketa bat proposatzen du egutegiak. Ostiralero CNRS blogeko Défis du Calendrier Mathématique atalean aste horretako ariketa bat aurki dezakezu.

[Buru Ariketa] 2020ko azken erantzuna